Localized,nonlinear,waves,in,a,myelinated,nerve,fiber,with,self-excitable,membrane

Nkeh Oma Nfor Patrick Guemkam Ghomsi and Francois Marie Moukam Kakmeni

1Department of Physics,HTTC Bambili,University of Bamenda,P.O.Box 39 Bambili,Cameroon

2Complex Systems and Theoretical Biology Group,Laboratory of Research on Advanced Materials and Nonlinear Science(LaRAMaNS),Department of Physics,Faculty of Science,University of Buea,P.O.Box 63 Buea,Cameroon

Keywords: myelinated nerve, Fitzhugh-Nagumo, capacitive feedback parameter, Ginzburg-Landau, collision,annihilation

There is a growing interest in recent years to investigate the nonlinear processing of information in reaction-diffusion systems, with sharp focus on neural networks.[1-6]From a biophysical perspective,the knowledge of neural information propagation mechanism constitutes one of the most interesting scientific challenges in excitable media.Generally speaking,an excitable system is one in which an initial stimulus of sufficient amplitude initiates a traveling wave propagating through the medium.[7,8]The mechanism of nerve impulse propagation was first investigated by Hodgkin-Huxley in 1952,[9,10]based on data from the squid giant axon for the space clamp membrane.This ionic model is highly physiological and governed by four nonlinear differential equations.Due to some computational difficulties encountered,Richard FitzHugh and Jin-ichi Nagumo independently proposed a simplified neuronal model of Hodgkin and Huxley known as the FitzHugh-Nagumo(FHN)model.[11,12]The FHN model is based on the Van Der Pol equations and mainly captures and crystallizes all the features of a dynamical system.

Concretely in the 1940s, Hodgkin, Huxley, and Katz mathematically and experimentally investigated the nature of nerve impulses.Their research revealed that the electrical pulses across the membrane arise from the uneven distribution between the intracellular fluid and the extracellular fluid of potassium(K+),sodium(Na+),and protein anions.[9,10,13]When a neuron is not emitting a signal,it is said to be at rest of roughly-70 mV and the interior part of the neuron is more negative with respect to the exterior.The variation in the Na+and K+permeability allows for the movement of ions in and out of the cell by means of opening and closing of various ion channels.The influx of Na+and efflux of K+results in electrical potential difference.Triggered by a stimulus the Na+channels open,the influx of Na+ions increases,the membrane depolarizes,and the potential voltage reaches a threshold level typically between-50 mV and-55 mV.At this moment an abrupt depolarization takes place,which rapidly moves the potential to a maximum of +30 mV.[9,10,13]At a similar rate,the Na+and K+channels close and open,respectively,initiating membrane repolarization caused by an efflux of K+ions,thereby causing the potential to drop back to resting state.During the repolarization process, the membrane goes through a transient hyperpolarization of-10 mV below resting potential.In a nutshell,all these changes in potential are physically depicted as an action potential,impulse or spike observed during the transmission of nerve impulses.

The above description of the action potential based on the Hodgkin-Huxley(HH)model is limited because it mainly assumes that the membrane capacitance is a constant.[9,10]However, experimental results suggest that the changes in membrane capacitance are of an order of magnitude sufficient to account for the observed voltage changes during the action potential.[14,15]This variation in membrane capacitance may emanate from changes in thickness and area (among other physiological factors) of the membrane during the action potential.Recent studies have been carried out to model the membrane capacitance as a nonlinear function of the transmembrane voltage (see, for example, Ref.[6] and references therein).Dikand´eet al.[6]considered two types of capacitance-voltage (C-V) characteristics, which are polynomial functions of the transmembrane voltage, and showed that the cytoplasm behaves like a self generative excitable medium during the transmission of nerve impulses.They further demonstrated that for both myelinated and unmyelinated nerve fibers, the nerve impulses are well-localized in spacetime coordinates with their shapes and stability determined by theC-Vcharacteristics.However, the present study clearly differs from the one carried out by Dikand´eet al.in the following three ways: (i)We focus mainly on a myelinated axon with a recovery mechanism.(ii) The ionic current is considered to be a nonlinear function of the transmembrane voltage.(iii) The issue of dissipation in the nerve fiber is addressed,which enables us to monitor the evolution of nerve impulse without significant distortion.Here the effects of dissipation clearly dominates that of linear dispersion, leading to a nonlinear diffusive process because of the interplay between nonlinearity and dissipation.Traveling pulses in dissipative systems is some times termed dissipative solitons, which were first predicted to exist in reaction-diffusion systems.[16]Dissipative and nonlinear effects are also crucial factors in reactiondiffusion systems,with the dissipative effect spreading though out a neural network because of the spatially localized connectivity between adjacent group of neurons.However, the dynamic balance between these two components usually generates diffusive solitons observed in most excitable media.

The conduction of action potential is physically manifested as the propagation of nerve impulse that maintains its amplitude, density, and velocity during the transmission of neuronal information along a conservative axon.The phenomenon of modulational instability, which is triggered by competitive effects of nonlinearity and dispersion in nonlinear systems,[17-20]is inextricably linked to the observation of soliton-like modes in neural networks.[1,4,5]Ever since the discovery of solitons by Fermi,Pasta,and Ulam,[17]enormous efforts have been made to elucidate on many complex phenomena in a plethora of nonlinear physical systems.This ranges from the propagation of femtosecond pulses in erbium doped fibers,[21]observation of first-order bright solitary waves in non-autonomous generalized AB system,[22,23]classification of solutions to the defocusing complex modified Korteweg-de Vries equation with the step-like initial condition,[24]among many others.

This study mainly presents an electrical diffusive lattice in the form of a transmission line that models the modified discrete FHN equations, which physically depicts a myelinated axon with nonlinear membrane capacitance.The mathematical study of spatially discrete models is challenging because of special and poorly understood phenomena occurring in them like propagation failure.In fact, this work is an extension of the one carried out in Ref.[4], with the exception that the membrane capacitance of the myelinated axon is now a polynomial function of transmembrane voltage.Hence this membrane is considered as a self-excitable organ with capacitive feedback parameter,α, used to modify the dynamics of the propagating modulated nerve impulses.We will thus derive the complex Ginzburg-Landau (CGL) amplitude equation from the modified discrete FHN model with the system of equation reduced to the dissipative nonlinear Schr¨odinger(DNLS)equation whenα=αcr(whereαcris the critical value of the capacitive feedback parameter).Bright solitary wave solutions of the DNLS equation are obtained,which enable us to observe the propagation of modulated nerve impulses in the myelinated axon at this critical value.

In Section 2, we describe an electrical circuit that represents a discrete FHN model with nonlinear membrane capacitance.By using Kirchhoff’s current and voltage laws,we derive the modified discrete FHN equation which is transformed to its Li´enard form.The model CGL amplitude equation is eventually obtained from the Li´enard equation using the multiple scale expansion in the semi-discrete approximation perturbation method.Modulational instability analysis is carried in Section 3, with results that fulfill the Benjamin-Feir criteria.This clearly shows that the modulated nerve impulses emanate from unstable plane wave solutions,with variation inαgenerally influencing the stability of plane waves.Analytic solutions of the derived amplitude equations lead to the observation of modulated nerve impulses.A numerical simulation scheme of the Li´enard form of the modified discrete FHN equation is carried out in Section 4,with initial condition being the solutions of the derived amplitude equations.Results of the numerical simulations mainly confirm the propagation,collision,and annihilation of nerve impulses in the myelinated axon,as the various relevant parameters are varied.Finally the main results are summarized in Section 5 with discussion and conclusion.

We consider a nonlinear electrical FHN lattice realized withNelementary cells,resistively coupled by linear resistorsRc, as represented in Fig.1.Each cell contains a nonlinear capacitor of capacitanceC(Un),a linear self-inductanceL,linear resistorR, a cellε, and a nonlinear resistor of resistanceRNL.The current-voltage characteristic of the nonlinear resistor obeys the following cubic law:[11,12]

whereR0andU0are normalization parameters withR0being a weighting resistor.This nonlinear resistorRNLis mostly constructed using analogue multipliers.

Fig.1.Schematic representation of the electrical lattice under consideration.The nonlinear resistance RNL and nonlinear capacitance C(Un)are functions of the transmembrane voltage.

Using Kirchhoff’s laws leads to the set of differential equations describing nonlinear propagation in the lattice,

whereUnandiL,nare the voltage and the resulting current,respectively, through the linear inductorLat thenth cell.By using the normalized variables:un=Un/U0,K=R0/Rc,vn=R0iL,n/U0,a=R20ε/LU20,b=R20/LU0,c=RR0/LU0andτ=U0/R0t,we transform Eq.(2)to a one-dimensional chain of modified discrete FHN equations:

Here we assume that the total charge on the membrane of the myelinated axon (i.e., the charge stored by the nonlinear membrane capacitor) is governed by the polynomial function[6]

wherec0is the constant value of the membrane capacitance,αis the capacitive feedback parameter having dimensions of inverse voltage squared.Physically,unis the membrane potential at thenth excitable membrane site known as Ranvier node whilevnis the corresponding recovery variable.Diffusive solitons as carriers of energy are well understood in conservative media, but the situation here is different because the medium is highly dissipative with the nonlinear ionic current insufficient to balance the energy outflow due to dissipation.This generates additional nonlinearity by spontaneously inducing the nerve membrane to manage the ionic charges with theCVcharacteristics given by Eq.(4).This measure is to maintain a stable diffusive solitary wave profile in the myelinated axon.[25-27]Note that forα=0,Eq.(3)is reduced to the wellknown FHN equations.[11,12]

The recovery variablevndepicts the slow dynamics because the parametersa,b,c ≪1.For Eq.(3a), the first term,un, accounts for the positive feedback, where depolarization enhances more depolarization through the voltage-gated sodium channel.The second term,-u3n/3, is a rapid negative feedback loop, corresponding to the auto-inactivation of the sodium channel.The third term,-vn,represents a recovery process, which may be physically responsible for regulating the outward potassium currents that oppose depolarization.The last term is the discrete diffusive term with coupling strengthK, which is proportional to the difference in internodal currents through a given Ranvier node.The first term in Eq.(3b), i.e.,a, mainly measures the potassium leakage current,whilebuncaptures the activation of the voltage-gated potassium channel by the membrane potentialun, which increases the magnitude ofvn.Lastly,-cvncontrols the pumping of potassium ions out of the neuron.

Differentiating Eq.(3a) with respect to time and substituting the value of ˙vnfrom Eq.(3b)yield

System (5) is therefore the Li´enard form of the modified discrete FHN model of a myelinated nerve fiber.ForD0=D1=0 andα=0, Eq.(5) becomes the cubic Li´enard equation with linear damping and it is sometimes regarded as a generalization of damped oscillations.Furthermore, within the linear regime and when the dissipation is neglected,we obtain the well-known linear harmonic oscillator that finds numerous applications in both classical and quantum physics.The Li´enard type of equations have been extensively investigated from both mathematical and physical perspectives,and their study remains an active field of research in mathematical physics.[4,5,28-30]

Since Eq.(5) is non-integrable, we proceed it by using a perturbation technique to find appropriate solutions.In this light, all the dissipative coefficientsγ2andD1are perturbed to the orderε2because of minimal damping,[5]whereε ≪1 is a slow variable parameter.Also, we greatly minimize the rate at which the leakage potassium ions are discharged from the neuron by perturbingγ0to orderε3.Consequently keeping just terms up to orderε2,Eq.(5)is rewritten as

Frequency limits exist within which normal propagation of nerve impulse signals is monitored across the modified discrete FHN axon.In order to identify the exact range of frequency, we introduce a perturbation method where a suitable solution of the modified FHN model containingεparameter is exploited.Upon substitution of this solution into the modified diffusive FHN model(6),the wave dispersion relation is obtained with terms at order ofε0eiθn.Hence,we consider a simplified solution of our modified discrete FHN model(6)of the form

withθn=qn-ωt,whereωis the angular frequency andqis the normal mode wave number.

In the perturbation approach known as the multiple scale expansion in the semidiscrete approximation,ψ(n,t) is supposedly independent of the “fast” variablestandn.Instead,it depend on the “slow” variables defined byXi=εixandTi=εit, fori ≥1.A continuum limit approximation is then employed with the wave amplitudes,while the discrete nature of the phase is maintained.Interested readers are advised to consult[5,31]for a comprehensive coverage of this perturbation technique.

Fig.2.Linear dispersion curve of the nerve impulse for D0=0.04 and Ω20 =0.032.There is a lower cutoff mode q=0 with frequency ω0 =Ω0 and upper cutoff mode q=π with frequency ωmax=(Ω20+4D0)1/2.

Collecting terms at orderε0eiθngives the dispersion relation

which is plotted in Fig.2.From Eq.(8), the linear spectrum has a gapωmin=Ω0and it is limited by the cut-off frequencyωmax=(Ω20+4D0)1/2due to discreteness.

Terms of orderε1eiθngives

wherevg=D0sinq/ωis the group velocity of the linear wave packets.

Finally,we collect terms proportional toε2eiθnto have

By considering the reference mobile frameξi=Xi-vgTiandτi=Tiwithvgbeing the group velocity of the wave,we obtain

wherePis the real dispersion coefficient,QrandQiare respectively the real and imaginary parts of the nonlinear coefficient,whileRis the dissipative coefficient.These parameters are given by

Equation (11) is the CGL equation, and broadly speaking, it represents one of the most-studied nonlinear equations in the scientific community today.This is because it gives a qualitative and quantitative description of a myriad of physical activities.[4,32,33]For example,in a diffusive Hindmarsh-Rose neural network,the propagation of modulated nerve impulses observed is also governed by the CGL equation,which clearly demonstrates how neurons participate in processing and sharing of information.[5]

The capacitive feedback parameter,α,clearly influences the nonlinearity of Eq.(11).ForQi＆gt;0 andQi＆lt;0, we are dealing with the nonlinear gain and nonlinear loss,and the dynamics of the system is still governed by the CGL equation.[4]WhenQivanishes,the value ofαis given by

Modulational instability is generally considered within our current context as a precursor for the generation of localized modulated nerve impulses in the myelinated axon.Consequently,we can now study perturbationsε(ξ1,τ2)≪1 of the continuous wave (cw) solution to the CGL Eq.(11) by using the ansatz[39,40]

We substitute this ansatz into the CGL Eq.(11), linearize inε, and look for solutions of the formε(ξ1,τ2) = [¯a(τ2)+i¯b(τ2)]cos(¯qξ1), which correspond to a weak perturbation of the intense cw background.Note that ¯qis the constant wavenumber of the perturbation and we obtain a linear system for ¯a(τ2)and ¯b(τ2)as

as depicted in Fig.3.The band of ¯qcrexponentially decreases with an increase in the dissipation of the medium,i.e.,the initial growth of modulational perturbations around the cw solution is being suppressed with increase in dissipation and time.

Fig.3.Variation of the critical wavenumber qcr with dissipation R,for P=Qr=1.00.

Fig.4.Product PQr of coefficients in Eq.(12)as functions of wave number q and capacitive feedback parameter α,for D0=D1=0.02,Ω20 =0.032,γ1=-0.15,γ2=0.001,c=1/3: (a)three-dimensional plot,(b)the corresponding contour plot,(c)α ＆lt;αcr,(d)α =αcr,(e)α ＆gt;αcr.

We have so far defined the behavior of the cw solutions whenη2(τ2)＆gt;0,η2(τ2)=0 andη2(τ2)＆lt;0.These processes capture and crystallize the stability dynamics of the system,which clearly tie in with the Benjamin-Feir criteria.The big problem now is to rigorously look for the most appropriate solution to Eq.(16)that matches exactly with all these predictions.In this light, we substitutex=exp[-Rτ2/2]and transform Eq.(16)into

whereσr=4Qr/R,σi=4Qi/Randθ2=P¯q2/4Qr.Equation(19)is the modified Bessel equation, and for the special case ofα=αcrwe haveσi=0,leading to solution[39]

whereIiσrθ2is the modified Bessel function withIiσrθ2＇denoting differentiation with respect to the argument.Asτ2→∞,solution in Eq.(20) reduces to ¯a(τ2)≈cos(σrθ2Rτ2/2+φ),

whereφis the phase difference.Becauseσrθ2Rτ2/2 =P¯q2τ2/2,it shows that solution(20)is most appropriate.

Figures 4(a) and 4(b) depict the three-dimensional plot of productPQrand the corresponding contour plot, as functions of wave numberqand capacitive feedback parameterα.It clearly captures and crystallizes regions of nonlinear excitations in the myelinated axon.In Fig.4(c) it is shown that forα＆lt;αcr,an increase in the wave numberqmainly favors the stability of plane waves in the myelinated axon.Figure 4(d) equally shows the same trend as in Fig.4(c), withα=αcr=1.00.The influence ofαon the stability of plane waves is clearly visible in Fig.4(e), whereα＆gt;αcr.For the caseα=1.25, once the critical wave number is exceeded, it becomes impossible to identify localized modes.However,an increase inαwith the case ofα=2.00 favors the generation of more localized modes,even when the wave number exceeds its critical value.These observations are consistent with the predictions made by Benjamin and Feir in fluid dynamics.[38]

The stability analysis just performed confirms the presence of localized wave packets in the myelinated axon,which we now proceed to analytically obtain the appropriate solutions.As the capacitive feedback parameterαis varied, we will consider two distinct solutions to the amplitude equation of motion.

3.1.Modulated impulses for α/=αcr and wavenumber q＆gt;0

Forα/=αcrand wavenumberq＆gt;0, the form of the solution to Eq.(11) that depicts modulated nerve nerves in the myelinated axon is given by[5,34,41,42]

where

A detailed analysis of spatial evolution of the modulated nerve impulses fort=0,20.0,40.0 is highlighted in Fig.5.Generally the form of the modulated nerve impulse is modified as time increases, with variation inαhaving minimal effects on this form.However,the amplitude of the modulated nerve impulse is greatly altered with variation inα.This is glaring with the transition ofαfrom 0.99 to 1.50 in Fig.5.This result suggests that the capacitive feed back parameterαis inextricably linked to the amplitude of the modulated nerve impulses in the myelinated axon,and ties in with the result obtained by Dikand´eet al.[6]

It should be noted that the spatial profile of the modulated nerve impulse solution (22) cannot be traced at lower cut off modeq=0.Furthermore,solution(22)remains undefined forα=αcr.Consequently we now seek for a specific solution in which these parameter values are valid, in order to fully account for the evolution of the modulated nerve impulses in the myelinated axon.

Fig.5.Evolution of modulated impulses according to Eq.(22)with ψ0=1.00,D0=D1=0.02,Ω20 =0.032,γ1=-0.15,γ2=0.001,c=1/3,q=ε =1.00,for various α.

3.2.Modulated impulses for α =αcr and at lower cut off mode(q=0)

Forα=αcrand at lower cut off mode(q=0),the form of the envelope soliton solution of Eq.(11), according to Ref.[37],is given by

whereX=X(ξ1,τ2)=ς0(τ2)ξ1+β0(τ2),withKbeing a real constant,χ(τ2),ς0(τ2),β0(τ2),andρ(τ2)are real functions of variableτ2to be defined anduis a real function of variableX.Inserting the ansatz(23)into Eq.(11)and separating the real and imaginary parts give

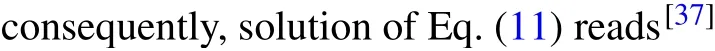
It is important to note thatρ0is an arbitrary real constant and we have setς00=1.00 without loss of generality.

We now show how the modulated nerve impulses propagate in the myelinated axon by substituting Eq.(33a) into solution(7)of the nerve impulse.We fix the valuesR=2.00,ψ0=1.00,K=20.0,K0=ρ0=0.00,Qr=2.00 andP=1.00 without loss of generality,but just to simplify the mathematical computations.This leads to

Recall thatξ1=ε(x-vgt),τ2=ε2t,x=nand at lower cutoff modeq=0,ω=Ω0,vg=0.This reduces solution(34)to the form

A plot of the spatial profile of the nerve impulses in the myelinated axon with the variation of the perturbation parameterεis given in Fig.6 at different time frames.It is also observed that the modulated impulses become more localized as the perturbationεincreases.For example, forε=0.100 as in the first diagram of Fig.6,the modulated impulses overlap,indicating that neuronal information is slowly transmitted in the myelinated axon.However, as the perturbation gradually increases toε=1.000 as in the last diagram of Fig.6,the neural signals are transmitted with high efficiency.This observation suggests that the flow of ionic charges within the neural membrane is greatly influenced by the variation of the perturbation parameterε.

Analysis of the time series dynamics of the nerve impulse fixed at the origin generates the curves in Fig.7.Also,as the perturbation increases, the nerve impulses gradually become more localized,suggesting that these perturbations physiologically affect the opening and closing of voltage-gated ion channels in the nerve membrane.In particular, forε=1.000, we observe a single spike which is qualitatively similar to those recorded in squid axons.[40]

Fig.6.Evolution of modulated impulses at lower cutoff mode(q=0),according to Eq.(35)with Ω0=0.18.The perturbation ε is varied.

Fig.7.Time series dynamics of the nerve impulse according to Eq.(35),when the perturbation parameter ε is varied.This is at lower cutoff mode q=0 and fixed at the origin(n=0)for Ω0=0.18.

The possibility of different outcomes with collision of nerve impulses in neural networks has greatly motivated the investigation of this phenomenon in this section.Action potentials are considered to be an electrical phenomenon,which is governed by the theoretical equations initially proposed by Hodgkin and Huxley.[10]Despite the numerous successes recorded by the HH model, it has been recently subjected to intense criticism.For example, it has been suggested that action potentials are a class of nonlinear waves called solitons,[43]which upon head-on collision, two solitons penetrate and continue to move with undistorted profile.Furthermore, penetration of two solitons propagating in a lipid bilayer membrane was also predicted in Ref.[43].However, a plethora of results[44-46]clearly indicates that pulse penetration is not observed in excitable membranes.Considering this evidence, it is unlike that action potentials are correctly described as solitons.It must be underscored that this does not cast doubt on the perception that an action potential is a nonlinear acoustic phenomenon.Other solitary waves like in Bose-Einstein condensates[47]and catalytic surface reactions,[48]annihilate upon head-on collision.Interestingly, annihilation however seems to be a comparatively rare scenario, suggesting that this phenomenon may require special type of nonlinearity in the medium of interaction.Furthermore, there are strong indications that excitable cells reside close to a phase transition.[49,50]If the latter incorporates the nonlinearity that allows for the generation of an action potential,the pulse could entail a phase change of the excitable medium.This transient realization of a different material phase may lead to pulse annihilation when two action potentials meet.In order to be able to penetrate, the pulses would have to propagate through this new phase.

4.1.Localized standing waves

We now numerically integrate Eq.(6), which is the Li´enard form of the modified discrete FHN equation.This is achieved by using the fifth-order Runge-Kutta scheme with a time step of 0.01, on a spatial domain supportingN=101 dynamical units,under periodic boundary conditions.To solve this non-integrable discrete nonlinear equation,we take,as initial condition, the analytical solution given by the modulated nerve impulse solution(22),which att=0.00 reads

On the upper part of Fig.8 for the given set of the system parameter values, it is observed that after sending the pulse ansatz in the system, the structure preserves this excitation state permanently with no event of propagation.This suggests that stationary localized pulses are accessible for our biological system.This solution is indeed an asymmetric localized solution which intimates the existence of a stable stationary bright envelope soliton solution for our modified discrete FHN model equation (6).Figures 8(a), 8(b), and 8(c)show the three-dimensional spatiotemporal display,the upper view, and the profile of this static pulse solution at all times,respectively.

Under other parameter conditions, this pulse solution turns into a localized standing wave.These are highlighted in Figs.8(d)-8(f).Figure 8(f) shows the standing wave profiles at different times.Further variations in the value of nonlinear coefficientγ1lead to different profiles of localized standing waves as reflected in Fig.9.

Fig.8.Membrane potential solutions of the modified discrete FHN Eq.(6) under two different parameters conditions.The upper figures depict a stationary localized pulse:(a)three-dimensional view,(b)upper view,(c)profile at all times.The parameters are taken as c=q=ε=1.00,α=0.0001,ψ0 =1.00, γ1 =0.05, γ2 =721.0, Ω20 =0.320, D0 =0.002, D1 =0.002.The lower figures depict a spatially localized standing wave: (d) threedimensional view, (e) upper view, (f) profiles of the wave at different times.The parameters values are the same as those in the upper figures, but γ2=0.00 and Ω20 =1.49.

Fig.9.Effects of variation in γ1 on the localized waves of the modified discrete FHN Eq.(6).The parameters are same as those in Fig.8 but for(a)γ1=0.001,(b)γ1=0.003,(c)γ1=0.045,and(d)γ1=0.050.

4.2.Propagation and collision

By varying the wave dispersion coefficientD0in the modified FHN neural network,we observe the profile of the waves as shown in Fig.10.

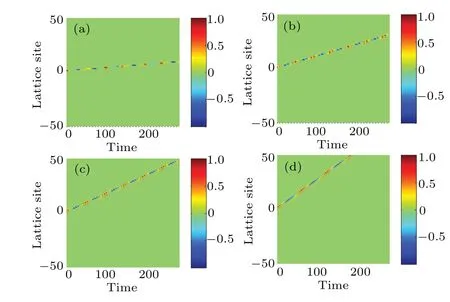
Fig.10.Effect of dispersion coefficient D0, on the propagation of action potential in the modified FHN model.The parameters are same as those in Fig.8 but for(a)D0=0.02,(b)D0=0.04,(c)D0=0.06,and(d)D0=0.08.

It is generally found that an increase inD0leads to a corresponding increase in the speed of propagation of nerve impulses.For the particular case in Fig.10(d),the nerve impulse takes just about 165 to move across the network.Based on these observations, we now plot the time of propagationτpand the propagation speedvp,as a function ofD0,as shown in Fig.11.

Figure 11(a)clearly shows that the time of propagationτpis inversely proportional to the dispersion coefficientD0,while Fig.11(b)depicts that the propagation speedvpincreases exponentially withD0.We further plot the spatial profiles of the nerve impulses at a particular value of dispersion coefficientD0,as shown in Fig.12.The spatial profiles of the nerve impulses in Fig.12(c)give the evolution from a pulse impulse att=0.00 to an asymmetric impulse att=206.4.

Fig.11.(a)Behavior of τp that is inversely proportional to D0,(b)behavior of vp that increases exponentially with D0.

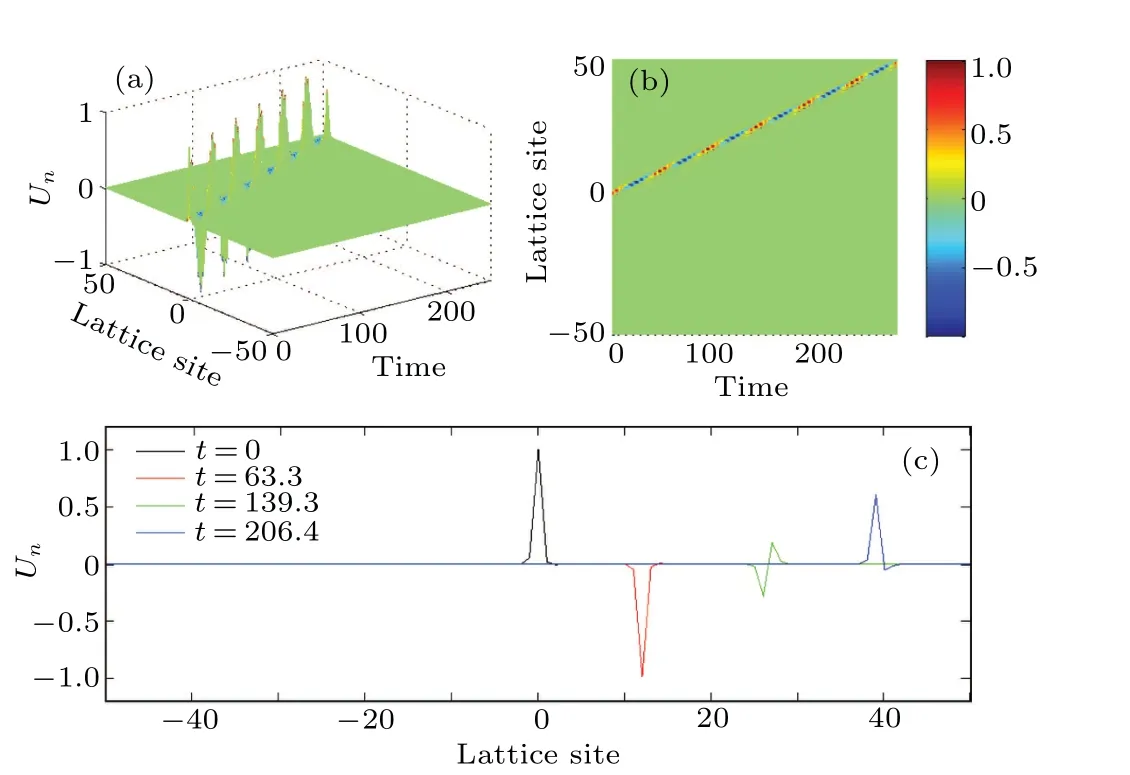
Fig.12.Propagation of the nerve impulses for dispersion coefficient D0 =0.06, as in Fig.10(c): (a) spatiotemporal evolution of nerve impulse,(b)the corresponding contour plot of the nerve impulse,(c)spatial profiles of the nerve impulse at different times.

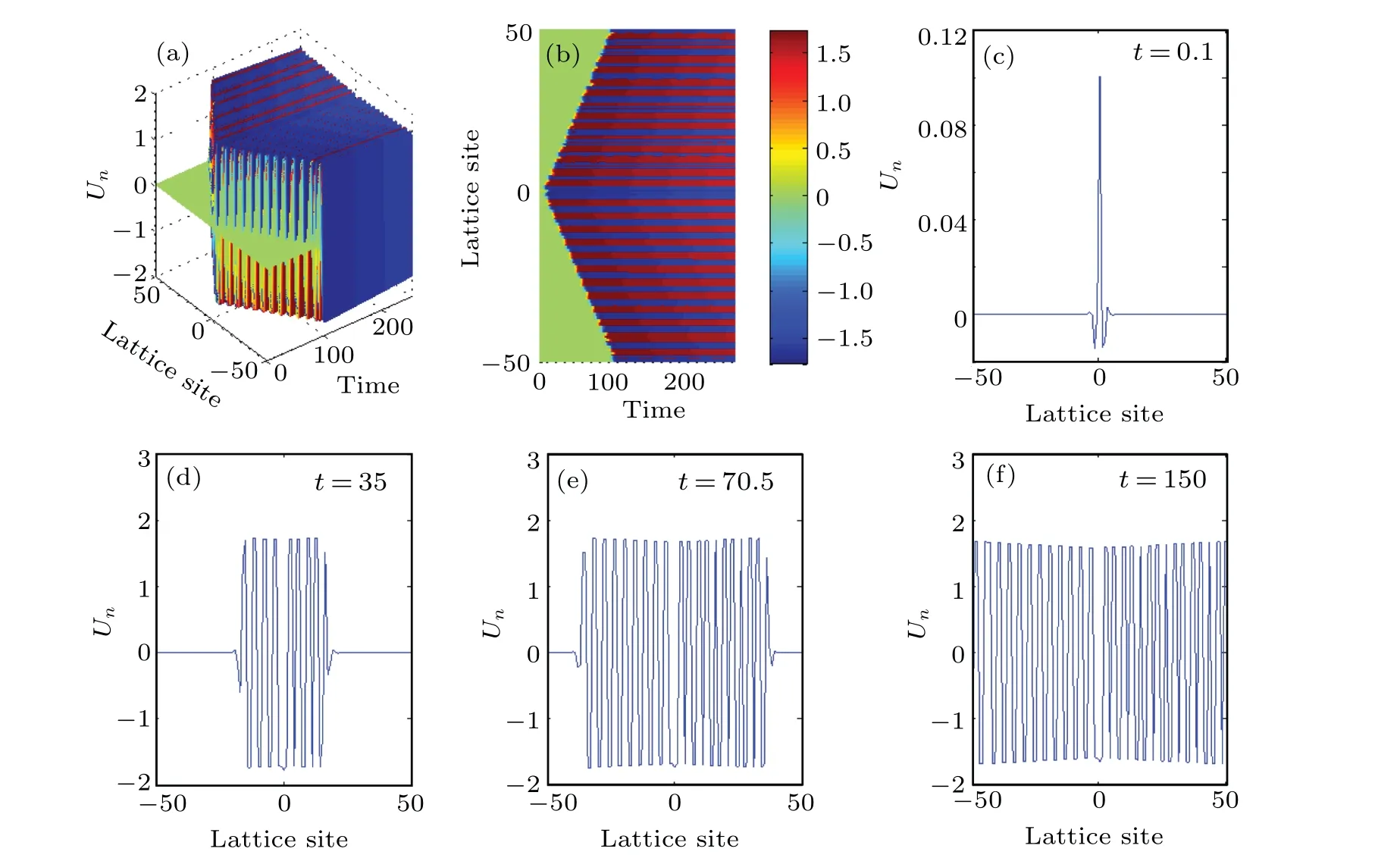
Fig.13.Collision of bi-pulse solution of the modified FHN Eq.(6):(a)three-dimensional view,(b)upper view,(c)profile at t=0.1,(d)profile at t=35,(e)profile at t=70.5,(f)profile at t=150.

By further choosing suitable parameters in the numerically integration of the modified discrete FHN Eq.(6), interesting behavior of the nerve impulse signal is revealed as in shown Fig.13.The pulse degenerates into a bi-soliton which propagates in opposite directions within the lattice of the myelinated axon.As a result of the imposed periodic boundary conditions, these two pulses collide at the boundaries of the neuronal lattice and annihilate each other.[1]Immediately after the annihilation,a dynamic structure known as multipulse crystal emerges in the myelinated axon.This multipulse solution is indeed a quadripulse,which can be viewed as being indicative of a localized firing state,with the occurrence of spatially localized static spiking structures in the neuronal network as in Fig.13(d) whent=35.These nerve impulse structures eventually evolve to occupy the entire lattice site as depicted in Fig.13(f)whent=150.

Soliton-like modes have already been identified in neural networks.For example, Moukamet al.reported on localized nonlinear excitations in diffusive Hindmarsh-Rose(HR) neural networks with nearest-neighbor linear electrical couplings.[5]On the other hand, Mvogoet al.considered the same HR network but with long-range diffusive coupling.[51]In both analyses, the neural membrane capacitance was assumed to be constant.However Dikand´eet al.considered a nonlinear membrane capacitance for both myelinated and unmyelinated nerve fibers, and showed that nerve impulses are well-localized in neural networks.[6]Our current investigation for single mode oscillations mainly deals with the modified FHN model.In fact we have considered an electrical lattice in the form of a nonlinear transmission line that models the modified discrete FHN system, in which the charge stored in the membrane,Q, is a nonlinear function of the trans-membrane voltage, i.e.,Q(un)=c0(1-αu2n)un.This nonlinear membrane capacitance is spontaneously induced during the generation and transmission of nerve impulse in the highly dissipative myelinated axon.The capacitive nonlinearity coupled with that of the ionic current dynamically competes with the highly dissipative effects experienced in the myelinated axon.By using the multiple scale expansion in the semi-discrete approximation,we have shown that the system of equation governing the propagation of modulated nerve impulses in the dissipative myelinated axon is the CGL amplitude equation.This equation is reduced to the DNLS equation at the critical value of the capacitive feedback parameter (i.e., atα=αcr).We equally investigate the modulational instability of the propagating nerve impulses, and confirm the predictions made by Benjamin and Feir in fluid dynamics.[38]The capacitive feedback parameterαplays a crucial role in plane wave stability.In fact, we find that the dissipation generally suppresses the modulational instability by switching the growth of the perturbations into an oscillatory behavior.This is graphically demonstrated in Fig.3,where the critical wavenumber ¯qcrdecreases with an increase in the dissipationR.The amplitude of the propagating modulated nerve impulses is generally altered with variation inα,suggesting that this parameter has a physiological effect on the ion channels in the membrane.Forα=αcr, the modulated nerve impulses are also identified in the myelinated axon(in both the spatial and time domains)at lower cutoff mode, which become more localized as the perturbation parameterεis increased.The results of numerical simulations of the modified discrete Fitzhugh-Nagumo equation show the propagation, collision, and annihilation of impulses in the neural network.

The ideal form of theC-Vcharacteristic is actually dictated by reliable experimental data on nerve impulse transmission under appropriate physiological conditions.However,an in-depth analysis involving available experimental data on the response of the nerve membrane capacitance to the transmembrane excitations is vital to gain complete qualitative as well as quantitative understandings of the nerve impulse generation and transmission in a myelinated axon with self excitable membrane.In this light, we believe that under appropriate physiological conditions, experimental investigations will shed more light on our current theoretical study carried out on a myelinated axon with self-excitable membrane.

Appendix A

Acknowledgements

The research activity carried out on neural dynamics with nonlinear membrane capacitance by Professor A.M.Dikand´e,greatly motivated N.Oma Nfor to initiate this project.

相关热词搜索：waves myelinated Localized